
Una soluzione per l'evento Tunguska
di Luigi Foschini
Traduzione dell'articolo pubblicato su Astron. Astrophys. 342, L1-L4 (1999)
Ricevuta: 1 settembre 1998 / Accettata: 10 Dicembre 1998
SOMMARIO
Questa lettera presenta una nuova soluzione per l'evento di Tunguska
del 30 giugno 1908. La soluzione è stata ottenuta a partire dai dati sismici, è in buon accordo
con le evidenze osservative, e è a favore della ipotesi di un'origine asteroidale del corpo
cosmico Tunguska. Si basa su un modello migliorato del flusso ipersonico intorno a un piccolo
asteroide nell'atmosfera terrestre.
Parole chiave: meteore, meteoroidi - pianeti minori, asteroidi.
1) INTRODUZIONE
Il 30 giugno 1908 qualcosa esplose sopra Tunguska, nella Siberia Centrale.
Nei passati novant'anni questo catastrofico evento ha ispirato una pletora di investigazioni
scientifiche. Nonostante molte scoperte interessanti, ci sono ancora delle sostanziali questioni
aperte ed inconsistenze circa le teorie e i dati disponibili (per una rivista vedi Vasilyev
1998).
Tra i molti diversi effetti, l'esplosione di Tunguska ha prodotto onde d'urto (shock waves) che
sono state registrate dai sismografi in diversi siti. Ben-Menahem
(1975) ha fatto una dettagliata
analisi di queste registrazioni sismiche e ha concluso che l'energia rilasciata nell'esplosione
era di 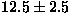 Mton. Ha anche concluso che i dati sulla fonte d'energia sono consistenti
con un'esplosione in atmosfera a un'altezza di circa 8.5 km. Mton. Ha anche concluso che i dati sulla fonte d'energia sono consistenti
con un'esplosione in atmosfera a un'altezza di circa 8.5 km.
In una precedente lettera (1998) abbiamo dimostrato che i dati sismici
possono essere usati per caratterizzare il bolide brillantissimo di Lugo del 1993, ottenendo
una buona corrispondenza tra le soluzioni ottenute e le osservazioni. La stessa metodologia
è applicata qui per analizzare l'evento di Tunguska, utilizzando le analisi di Ben-Menahem come
punto di partenza.
2) MODELLI CORRENTI
Molti diversi modelli sono stati sviluppati al fine di collegare i dati
disponibili dell'evento di Tunguska (per esempio, Chyba et al. 1993,
Grigoryan 1998, Hills e Goda 1993,
Lyne et al. 1996).
Tutti questi modelli hanno contribuito in modo significativo a migliorare la nostra conoscenza
sulla disgregazione dei meteoroidi nell'atmosfera. Questi modelli presumono generalmente che il
processo di frammentazione inizi quando la pressione aerodinamica è uguale alla resistenza
meccanica S del corpo cosmico. Ponendo in relazione la densità dell'aria con l'altezza
dell'esplosione, questo permette di stabilire la velocità del meteoroide (V):
|
| ![\begin{displaymath}V=\sqrt{\frac{S}{\rho_{\mathrm{sl}}}\exp\left[\frac{h}{H}\right]}\, ,\end{displaymath}](images/img2.gif) |
(1) |
dove 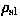 è la densità
atmosferica al livello del mare, h è l'altezza della prima frammentazione e H è
l'altezza di scala dell'atmosfera (circa 8 km).
Dalle analisi di Ben-Menahem, si deduce che c'è stato un singolo evento di frammentazione; non
ci sono prove di esplosioni multiple, come dovrebbe succedere durante eventi di frammentazioni
multiple (Ben-Menahem 1975). Di conseguenza,
l'equazione 1 può essere usata per derivare V, assumendo che la prima frammentazione
coincida con l'esplosione in atmosfera avvenuta a h=8.5 km. è la densità
atmosferica al livello del mare, h è l'altezza della prima frammentazione e H è
l'altezza di scala dell'atmosfera (circa 8 km).
Dalle analisi di Ben-Menahem, si deduce che c'è stato un singolo evento di frammentazione; non
ci sono prove di esplosioni multiple, come dovrebbe succedere durante eventi di frammentazioni
multiple (Ben-Menahem 1975). Di conseguenza,
l'equazione 1 può essere usata per derivare V, assumendo che la prima frammentazione
coincida con l'esplosione in atmosfera avvenuta a h=8.5 km.
Per diversi tipi di corpi cosmici, corrispondenti a diversi valori assunti per S (preso
da Hills e Goda 1993), otteniamo i risultati listati in tabella 1.
| Body type (tipologia del corpo) |
S [Pa] |
V [km/s] |
| Comet (cometa) |
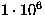 |
1.5 |
| Carbonaceous chondrite (condrite carbonacea) |
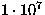 |
4.7 |
| Stone (roccia) |
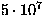 |
10.6 |
| Iron (ferro) |
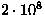 |
21.2 |
Tabella 1 - Velocità del corpo cosmico di Tunguska in rapporto alla resistenza in
base all'Eq. 1
Ora, dato che fino a poco prima dell'esplosione i grandi meteoroidi sono
sottoposti a una limitata perdita di massa durante il loro cammino atmosferico, la velocità
prima dell'esplosione deve essere vicina alla velocità orbitale (geocentrica), e questa deve
essere superiore alla velocità di fuga dalla Terra (11.2 km/s).
Quindi, in base ai risultati derivati dall'equazione 1, la soluzione più plausibile sarebbe
quella di un corpo ferroso. Tuttavia l'ipotesi del corpo ferroso non è consistente con i recenti
ritrovamenti sul sito di rimanenze microscopiche di un oggetto pietroso (Longo et al.
1994, Serra et al. 1994).
Attualmente, prendendo per buona l'incertezza nella valutazione di S e dei diversi errori
di misurazione (entrambi difficili da quantificare), la soluzione per gli oggetti pietrosi non
può essere interamente esclusa usando questo argomento (le tipiche velocità geocentriche per gli
asteroidi Near-Earth sono circa 15 km/s). Tuttavia è risaputo che l'interazione di grandi
meteoroidi (o piccoli asteroidi) con l'atmosfera terrestre è caratterizzata da una grande
varietà di comportamenti, e qualunque teoria quantitativa dovrebbe prendere in considerazione un
grande numero di variabili: dimensione, forma, rotazione, composizione, struttura interna,
velocità orbitale, angolo di volo. Quindi, attualmente ogni bolide può essere visto come un caso
di studio, che può portare argomenti utili per una futura teoria generale.
Come ulteriore conseguenza l'equazione 1 non può essere considerata utile per ottenere risultati
quantitativamente credibili per ogni episodio. Di fatto sappiamo che talvolta gli asteroidi
esplodono a una pressione dinamica molto più bassa della loro resistenza dinamica (Ceplecha [1995).
Nel caso del bolide di Lugo, un'interessante possibilità è che questo comportamento sia in
relazione alla struttura porosa del meteoroide (Foschini 1998).
Tuttavia la Tabella 1 mostra che nel caso di Tunguska abbiamo il problema opposto e che dovremmo
presumere una resistenza meccanica eccezionalmente elevata. Quindi io guarderò in un'altra
direzione per una possibile soluzione del problema.
3) FLUSSO IPERSONICO
Quando un grande meteoroide entra nell'atmosfera terrestre, ha una
velocità compresa tra 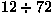 km/s, e quindi si muove
a velocità ipersonica (cioè, con un numero di Mach maggiore di 5). Dato che siamo interessati
alla dinamica di un meteoroide grande a sufficienza da raggiungere la bassa atmosfera, il fluido
che può essere trattato come un continuo. Perciò possiamo usare le attuali conoscenze
sull'aerodinamica ipersonica, per comprendere le esplosioni in atmosfera dei meteoroidi.
Per ulteriori esposizioni di questa teoria, il lettore si riferisca ai libri di Shapiro
(1954, Landau & Lifshitz
(1987) e Holman (1989). km/s, e quindi si muove
a velocità ipersonica (cioè, con un numero di Mach maggiore di 5). Dato che siamo interessati
alla dinamica di un meteoroide grande a sufficienza da raggiungere la bassa atmosfera, il fluido
che può essere trattato come un continuo. Perciò possiamo usare le attuali conoscenze
sull'aerodinamica ipersonica, per comprendere le esplosioni in atmosfera dei meteoroidi.
Per ulteriori esposizioni di questa teoria, il lettore si riferisca ai libri di Shapiro
(1954, Landau & Lifshitz
(1987) e Holman (1989).
E' importante notare che per grandi numeri di Mach le equazioni linearizzate per la velocità
potenziale non sono valide, per cui non possiamo usare le leggi valide per le velocità
supersoniche. Nel flusso ipersonico, le onde di Mach e le onde d'urto oblique sono emesse a
piccole angolazioni in direzione del flusso, dell'ordine di grandezza del rapporto tra lo
spessore e la lunghezza del corpo, per cui tendono a seguire la superficie del corpo. In queste
condizioni, la traiettoria atmosferica di un grande meteoroide può essere vista come un lungo
cilindro, generante onde di pressione che possono essere captate come suoni infrasonici
(Cumming 1989, ReVelle 1976).
Il piccolo angolo di Mach e le onde d'urto oblique danno anche origine al concetto di strato
limite ipersonico vicino alla superficie. Davanti al meteoroide c'è un arco d'urto, che avviluppa
il corpo. L'urto è più forte sull'asse di simmetria, perché in quel punto è normale al flusso.
Poi troviamo una zona dove la dissociazione molecolare è il processo principale e, anche più
vicino alla superficie del corpo, troviamo lo strato limite, dove gli effetti viscosi sono
dominanti. Mentre l'aria scorre verso la parte posteriore del meteoroide, essa è riattratta
verso l'asse, proprio come in un'espansione di Prandtl-Meyer. Come conseguenza, c'è una
rotazione del flusso nel senso opposto a quello del moto (rettificazione); questo crea un'onda
d'urto obliqua, che è chiamata urto di scia. Dato che la crescita di pressione lungo l'arco
d'urto è molto grande rispetto al calo di pressione nell'espansione di Prandtl-Meyer, si può
assumere, con ragionevole approssimazione, che c'è il vuoto nella parte posteriore del
meteoroide. Per immagini illustrative di un flusso ipersonico, ci riferiamo al capitolo 19,
volume 2, del libro di Shapiro (1954).
La temperatura del fluido aumenta nello strato limite, perché la velocità deve decrescere a zero
sulla superficie del meteoroide; inoltre ci sono effetti di riscaldamento dovuti alla
dissipazione viscosa. Ci sono inoltre regioni (come nell'espansione Prandlt-Meyer) nelle quali
la presenza del vuoto o quasi-vuoto riduce fortemente la trasmissione del calore, e questo
contribuisce a incrementare la temperatura del corpo. Se la generazione del calore aumenta
così velocemente che la perdita di calore può essere inadeguata a stabilire uno stato di
equilibrio, possiamo avere un'esplosione termica. Questa esplosione genera onde di pressione che
possono essere captate sul terreno dai sismografi. Da notare che dopo l'evento di Tunguska
nessun meteorite è stato recuperato, così, in questo caso, l'argomento che i meteoriti sono
solitamente freddi dopo l'impatto non costituisce prova contro questo tipo di esplosioni
termiche.
I modelli correnti dell'evento di Tunguska considerano come punto di riferimento solamente
la pressione di stagnazione (per esempio, Hills & Goda 1993),
anche se, per le ragioni sottolineate sopra, una descrizione fisica realistica dovrebbe tenere
presente i processi di generazione e trasmissione del calore. Una simile conclusione, sulla
necessità di modelli accoppiati radiativo-idrodinamici, è stato recentemente raggiunto da
Borovicka e altri (1998a,
1998b), seguendo una dettagliata analisi
delle teorie e osservazioni del bolide di Benesov.
4) L'IMPORTANZA DELLA TEMPERATURA DI STAGNAZIONE
Consideriamo ora il riscaldamento dovuto alla conversione dell'energia
cinetica del flusso in energia termica, quando il gas è portato a riposo (nello stato limite).
Questo processo può essere descritto in termini di un flusso costante di energia in un processo
adiabatico:
|
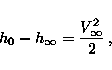 |
(2) |
dove h0 e 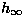 sono rispettivamente l'entalpia nel punto di stagnazione e del flusso libero, e
sono rispettivamente l'entalpia nel punto di stagnazione e del flusso libero, e 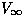 è la velocità del flusso non perturbato. Da
notare che la scelta del sistema di riferimento non è importante: se noi consideriamo un
sistema di riferimento centrato sul corpo, il fluido sarà in movimento, e viceversa; di
conseguenza è la velocità del flusso non perturbato. Da
notare che la scelta del sistema di riferimento non è importante: se noi consideriamo un
sistema di riferimento centrato sul corpo, il fluido sarà in movimento, e viceversa; di
conseguenza 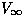 può essere interpretata
come la velocità del corpo rispetto all'atmosfera. Possiamo riscrivere l'equazione 2 in termini di temperatura: può essere interpretata
come la velocità del corpo rispetto all'atmosfera. Possiamo riscrivere l'equazione 2 in termini di temperatura:
|
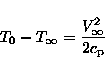 |
(3) |
dove 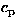 è il calore specifico a pressione costante. Durante il
percorso atmosferico, dato che il numero di Mach è molto elevato, la velocità del meteoroide è prossima al valore massimo corrispondente
alla temperatura di stagnazione. Cambiamenti nelle proprietà del flusso sono dovute principalmente a cambiamenti nella temperatura di
stagnazione T0, che è una misura diretta dell'ammontare della trasmissione di calore. è il calore specifico a pressione costante. Durante il
percorso atmosferico, dato che il numero di Mach è molto elevato, la velocità del meteoroide è prossima al valore massimo corrispondente
alla temperatura di stagnazione. Cambiamenti nelle proprietà del flusso sono dovute principalmente a cambiamenti nella temperatura di
stagnazione T0, che è una misura diretta dell'ammontare della trasmissione di calore.
Questo argomento sottolinea l'importanza della temperatura di stagnazione nel flusso ipersonico,
dal momento che è in relazione con la massima velocità del flusso, che, a sua volta, è legata
alla velocità del corpo cosmico. In base a Shapiro (1954),
la relazione tra la temperatura di stagnazione e la velocità massima del flusso può essere espressa nella seguente maniera:
|
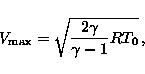 |
(4) |
dove 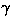 è il rapporto tra i calori
specifici. Per mezzo dell'equazione di stato per l'aria, Vmax
può essere espressa in funzione della pressione e della densità nel punto di stagnazione: è il rapporto tra i calori
specifici. Per mezzo dell'equazione di stato per l'aria, Vmax
può essere espressa in funzione della pressione e della densità nel punto di stagnazione:
|
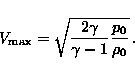 |
(5) |
Al fine di ottenere una condizione per la frammentazione del meteoroide, la pressione di stagnazione
p0 deve essere uguale alla resistenza meccanica S del corpo.
Per la densità di stagnazione abbiamo (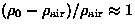 (Landau & Lifshitz 1987), dove
(Landau & Lifshitz 1987), dove
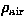 è la densità
dell'aria indisturbata all'altezza di esplosione. Finalmente, esprimendo è la densità
dell'aria indisturbata all'altezza di esplosione. Finalmente, esprimendo
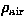 in funzione
dell'altezza in atmosfera h e in funzione
dell'altezza in atmosfera h e 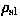 ,
come nell'equazione 1, otteniamo una nuova equazione per stimare Vmax,
che è prossimo alla velocità V del corpo cosmico alla frammentazione: ,
come nell'equazione 1, otteniamo una nuova equazione per stimare Vmax,
che è prossimo alla velocità V del corpo cosmico alla frammentazione:
|
![\begin{displaymath}V\approx V_{\mathrm{max}}=\sqrt{\frac{\gamma}{\gamma-1}\frac{S}{\rho_{\mathrm{sl}}} \exp\left[\frac{h}{H}\right]}\, .\end{displaymath}](images/img21.gif) |
(6) |
Per 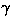 possiamo usare un valore
di circa 1,7 risultato da studi sperimentali sul plasma sviluppato in impatti iperveloci (Kadono &
Fujiwara 1996). Comparando l'equazione 6 all'equazione 1 possiamo vedere un fattore addizionale
1,6 circa. Ciò deriva dal fatto che l'equazione 6 deriva dall'equazione 4, secondo cui, quando
un corpo sta viaggiando alla velocità ipersonica, la temperatura di stagnazione dipende dalla
velocità. L'Equazione 6 mostra che l'esplosione in atmosfera avviene grazie alla combinazione di
effetti termici e meccanici che agiscono sul meteoroide. In altre parole, i processi termodinamico
abbassano in modo significativo la pressione effettiva che schiaccia il corpo, così lo stesso
corpo può raggiungere un'altitudine più bassa, oppure per una data altezza di esplosione, occorre
una resistenza più bassa. possiamo usare un valore
di circa 1,7 risultato da studi sperimentali sul plasma sviluppato in impatti iperveloci (Kadono &
Fujiwara 1996). Comparando l'equazione 6 all'equazione 1 possiamo vedere un fattore addizionale
1,6 circa. Ciò deriva dal fatto che l'equazione 6 deriva dall'equazione 4, secondo cui, quando
un corpo sta viaggiando alla velocità ipersonica, la temperatura di stagnazione dipende dalla
velocità. L'Equazione 6 mostra che l'esplosione in atmosfera avviene grazie alla combinazione di
effetti termici e meccanici che agiscono sul meteoroide. In altre parole, i processi termodinamico
abbassano in modo significativo la pressione effettiva che schiaccia il corpo, così lo stesso
corpo può raggiungere un'altitudine più bassa, oppure per una data altezza di esplosione, occorre
una resistenza più bassa.
5) UNA NUOVA ANALISI DELL'EVENTO DI TUNGUSKA
Per mezzo dell'equazione 6 possiamo rimpiazzare la tabella 1 con una
nuova tabella per le velocità di frammentazione di diversi tipi di corpi cosmici (vedi tabella 2).
| Body Type |
S [Pa] |
V [km/s] |
| Comet |
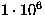 |
2.3 |
| Carbonaceous Chondrite |
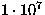 |
7.4 |
| Stone |
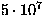 |
16.5 |
| Iron |
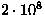 |
33.0 |
Tabella 2 - Velocità del corpo cosmico di Tunguska in rapporto alla
resistenza secondo l'equazione 6
Da notare che adesso la velocità dedotta di un corpo ferroso risulta
essere troppo alta, e che i corpi pietrosi forniscono la soluzione più plausibili. Questo è
compatibile con i risultati di una dettagliata analisi di diverse centinaia di meteore effettuata
da Ceplecha e McKrosky (1976) e Ceplecha
(1994), che hanno trovato che un'altezza attorno ai
10 km è tipica per corpi rocciosi.
Possiamo adesso calcolare altri dati per l'evento di Tunguska, risolvendo le equazioni di
movimento e luminosità, in base alle procedure descritte da Foschini (1998). I risultati sono
riassunti in tabella 3. Sono state fatte le seguenti ipotesi: (i) l'efficienza luminosa
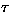 è del 5%; (ii) il diametro
dell'oggetto è calcolato supponendo una forma sferica e una densità di 3.500 kg/m3,
tipica di un oggetto roccioso. è del 5%; (ii) il diametro
dell'oggetto è calcolato supponendo una forma sferica e una densità di 3.500 kg/m3,
tipica di un oggetto roccioso.
Apparition time (UT)
 |
1908-06-30 00:14:28 UT |
Latitude of airburst
 |
60° 55' N |
Longitude of airburst
 |
101° 57' E |
Airburst height
 |
8.5 km |
Explosion Energy
 |
12.5 Mton |
| Mass |
4*108 kg |
| Diameter |
60 m |
| Abs. Visual Magnitude |
-29.4 |
| Velocity |
16.5 km/s |
Inclination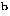 |
3° |
Path azimuth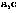 |
115° |
- [
 ]
From Ben-Menahem ([1975]). ]
From Ben-Menahem ([1975]).
- [
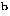 ] Over the horizon. ] Over the horizon.
- [
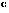 ] Clockwise from North. ] Clockwise from North.
Tabella 3 - Elenco delle caratteristiche del corpo cosmico di Tunguska
Comparando questi risultati con quelli precedenti e con i dati a disposizione (per
una rivista vedi Vasilyev 1998),
notiamo generalmente un buon accordo, tranne che per l'inclinazione sopra l'orizzonte della
traiettoria. Il valore ottenuto qui è circa 3°, mentre Vasilyev riporta che l'angolo
d'inclinazione più probabile era circa di circa 15°. Tuttavia egli ha anche notato la
possibilità di una buona forma aerodinamica del corpo cosmico di Tunguska, che può avere
ridotto l'angolo d'inclinazione. Inoltre, abbiamo trascurato gli effetti di sollevamento,
seguendo Chyba e altri (1993).
Tra gli autori citati da Vasilyev, solo Sekanina ha derivato un angolo inferiore a 5°.
E' interessante notare che proprio Sekanina (1998)
ha fortemente favorito la conclusione di un'origine asteroidale del corpo cosmico di Tunguska.
I risultati qui ottenuti danno un ulteriore supporto alle conclusioni di Sekanina.
6) CONCLUSIONI
In questo articolo, abbiamo delineato una nuova analisi dell'evento di
Tunguska, partendo dai dati sismici ottenuti da Ben-Menahem (1975)
e migliorando la relazione tra velocità del corpo, resistenza meccanica e l'altezza
dell'esplosione. Le principali conclusioni sono che il corpo cosmico di Tunguska era
probabilmente un asteroide roccioso con un diametro di circa 60 m.
Abbiamo inoltre riassunto le proprietà del flusso ipersonico intorno a un piccolo asteroide
nell'atmosfera terrestre. Abbiamo dimostrato che la temperatura di stagnazione è una diretta
misura della velocità del corpo. Questo introduce un fattore moltiplicativo di
(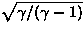 )
nell'equazione 1, che è indispensabile per derivare una soluzione ragionevole dell'evento di
Tunguska. L'equazione 6 è coerente con l'idea che la frammentazione del meteoroide è dovuta
all'azione accoppiata di processi termodinamici e meccanici. )
nell'equazione 1, che è indispensabile per derivare una soluzione ragionevole dell'evento di
Tunguska. L'equazione 6 è coerente con l'idea che la frammentazione del meteoroide è dovuta
all'azione accoppiata di processi termodinamici e meccanici.
Questo tipo di analisi può essere applicata ogni volta che il corpo è grande e compatto abbastanza
da raggiungere la bassa atmosfera. Ulteriori ricerche sono necessarie per applicarla agli altri
casi. Tuttavia, il ruolo cruciale della temperatura di stagnazione è probabilmente una
caratteristica generale di ogni modello realistico del volo e della rottura di un meteoroide.
Ringraziamenti:
l'autore ringrazia un anonimo referee per i suoi utili commenti.
Un ringraziamento particolare a Paolo Farinella per una costruttiva revisione.
Riferimenti bibliografici (References)
- 1975
- Ben-Menahem A., 1975, Phys. Earth Planet. Inter. 11, 1
- 1998a Borovicka J., Popova O.P., Nemtchinov I.V., Spurný P., Ceplecha Z., 1998a, A&A 334, 713
- 1998b Borovicka J., Popova O.P., Golub' A.P., Kosarev I.B., Nemtchinov I.V., 1998b, A&A 337, 591
- 1994
- Ceplecha Z., 1994, A&A 286, 967
- 1995
- Ceplecha Z., 1995, Earth, Moon, Planets 68, 107
- 1976
- Ceplecha Z., McCrosky R.E., 1976, J. Geophys. Res. 81, 6257
- 1993
- Chyba C.F., Thomas P.J., Zahnle K.J., 1993, Nature 361, 40
- 1989
- Cumming G.L., 1989, Can. J. Earth Sci. 26, 1350
- 1998
- Foschini L., 1998, A&A 337, L5
- 1998
- Grigorian S.S., 1998, Planet. Space Sci. 46, 213
- 1993
- Hills J.G., Goda M.P., 1993, AJ 105, 1114
- 1989
- Holman J.P., 1989, Heat transfer, McGraw-Hill, Singapore.
- 1996
- Kadono T., Fujiwara A., 1996, J. Geophys. Res. 101, 26097.
- 1987
- Landau L.D., Lifshitz E.M., 1987, Course of Theoretical Physics - vol. 6: Fluid mechanics, 2nd rev. ed., Butterworth-Heinemann, Oxford.
- 1994
- Longo G., Serra R., Cecchini S., Galli M., 1994, Planet. Space Sci. 42, 163
- 1996
- Lyne J.E., Tauber M., Fought R., 1996, J. Geophys. Res. 101, 23207
- 1976
- ReVelle D.O., 1976, J. Geophys. Res. 81, 1217
- 1998
- Sekanina Z., 1998, Planet. Space Sci. 46, 191
- 1994
- Serra R., Cecchini S., Galli M., Longo G., 1994, Planet. Space Sci. 42, 777
- 1954
- Shapiro A.H., 1954, The dynamics and thermodynamics of compressible fluid flow, 2 vols., The Ronald Press Company, New York.
- 1998
- Vasilyev N.V., 1998, Planet. Space Sci. 46, 129
Commento di Luigi Foschini all'evento di Tunguska (30 giugno 2008)
Impact '99 |
Articoli |
Fotografia, ccd e ricerca
Homepage
Copyright © 1998 di Luigi Foschini; impaginazione web di Lucio Furlanetto

Pagina caricata in rete: 26 gennaio 2002; ultimo aggiornamento (5°): 18 novembre 2008
|

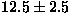 Mton. Ha anche concluso che i dati sulla fonte d'energia sono consistenti
con un'esplosione in atmosfera a un'altezza di circa 8.5 km.
Mton. Ha anche concluso che i dati sulla fonte d'energia sono consistenti
con un'esplosione in atmosfera a un'altezza di circa 8.5 km. ![\begin{displaymath}V=\sqrt{\frac{S}{\rho_{\mathrm{sl}}}\exp\left[\frac{h}{H}\right]}\, ,\end{displaymath}](images/img2.gif)
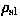 è la densità
atmosferica al livello del mare, h è l'altezza della prima frammentazione e H è
l'altezza di scala dell'atmosfera (circa 8 km).
Dalle analisi di Ben-Menahem, si deduce che c'è stato un singolo evento di frammentazione; non
ci sono prove di esplosioni multiple, come dovrebbe succedere durante eventi di frammentazioni
multiple (Ben-Menahem
è la densità
atmosferica al livello del mare, h è l'altezza della prima frammentazione e H è
l'altezza di scala dell'atmosfera (circa 8 km).
Dalle analisi di Ben-Menahem, si deduce che c'è stato un singolo evento di frammentazione; non
ci sono prove di esplosioni multiple, come dovrebbe succedere durante eventi di frammentazioni
multiple (Ben-Menahem 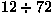 km/s, e quindi si muove
a velocità ipersonica (cioè, con un numero di Mach maggiore di 5). Dato che siamo interessati
alla dinamica di un meteoroide grande a sufficienza da raggiungere la bassa atmosfera, il fluido
che può essere trattato come un continuo. Perciò possiamo usare le attuali conoscenze
sull'aerodinamica ipersonica, per comprendere le esplosioni in atmosfera dei meteoroidi.
Per ulteriori esposizioni di questa teoria, il lettore si riferisca ai libri di Shapiro
(
km/s, e quindi si muove
a velocità ipersonica (cioè, con un numero di Mach maggiore di 5). Dato che siamo interessati
alla dinamica di un meteoroide grande a sufficienza da raggiungere la bassa atmosfera, il fluido
che può essere trattato come un continuo. Perciò possiamo usare le attuali conoscenze
sull'aerodinamica ipersonica, per comprendere le esplosioni in atmosfera dei meteoroidi.
Per ulteriori esposizioni di questa teoria, il lettore si riferisca ai libri di Shapiro
(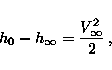
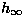 sono rispettivamente l'entalpia nel punto di stagnazione e del flusso libero, e
sono rispettivamente l'entalpia nel punto di stagnazione e del flusso libero, e 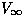 è la velocità del flusso non perturbato. Da
notare che la scelta del sistema di riferimento non è importante: se noi consideriamo un
sistema di riferimento centrato sul corpo, il fluido sarà in movimento, e viceversa; di
conseguenza
è la velocità del flusso non perturbato. Da
notare che la scelta del sistema di riferimento non è importante: se noi consideriamo un
sistema di riferimento centrato sul corpo, il fluido sarà in movimento, e viceversa; di
conseguenza 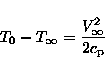
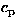 è il calore specifico a pressione costante. Durante il
percorso atmosferico, dato che il numero di Mach è molto elevato, la velocità del meteoroide è prossima al valore massimo corrispondente
alla temperatura di stagnazione. Cambiamenti nelle proprietà del flusso sono dovute principalmente a cambiamenti nella temperatura di
stagnazione T0, che è una misura diretta dell'ammontare della trasmissione di calore.
è il calore specifico a pressione costante. Durante il
percorso atmosferico, dato che il numero di Mach è molto elevato, la velocità del meteoroide è prossima al valore massimo corrispondente
alla temperatura di stagnazione. Cambiamenti nelle proprietà del flusso sono dovute principalmente a cambiamenti nella temperatura di
stagnazione T0, che è una misura diretta dell'ammontare della trasmissione di calore. 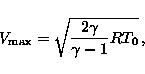
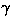 è il rapporto tra i calori
specifici. Per mezzo dell'equazione di stato per l'aria, Vmax
può essere espressa in funzione della pressione e della densità nel punto di stagnazione:
è il rapporto tra i calori
specifici. Per mezzo dell'equazione di stato per l'aria, Vmax
può essere espressa in funzione della pressione e della densità nel punto di stagnazione:
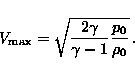
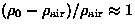 (Landau & Lifshitz
(Landau & Lifshitz 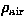 è la densità
dell'aria indisturbata all'altezza di esplosione. Finalmente, esprimendo
è la densità
dell'aria indisturbata all'altezza di esplosione. Finalmente, esprimendo
![\begin{displaymath}V\approx V_{\mathrm{max}}=\sqrt{\frac{\gamma}{\gamma-1}\frac{S}{\rho_{\mathrm{sl}}} \exp\left[\frac{h}{H}\right]}\, .\end{displaymath}](images/img21.gif)
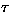 è del 5%; (ii) il diametro
dell'oggetto è calcolato supponendo una forma sferica e una densità di 3.500 kg/m3,
tipica di un oggetto roccioso.
è del 5%; (ii) il diametro
dell'oggetto è calcolato supponendo una forma sferica e una densità di 3.500 kg/m3,
tipica di un oggetto roccioso.
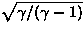 )
nell'equazione 1, che è indispensabile per derivare una soluzione ragionevole dell'evento di
Tunguska. L'equazione 6 è coerente con l'idea che la frammentazione del meteoroide è dovuta
all'azione accoppiata di processi termodinamici e meccanici.
)
nell'equazione 1, che è indispensabile per derivare una soluzione ragionevole dell'evento di
Tunguska. L'equazione 6 è coerente con l'idea che la frammentazione del meteoroide è dovuta
all'azione accoppiata di processi termodinamici e meccanici. 