CORREZIONE ELIOCENTRICA
La correzione eliocentrica è il valore temporale che occorre aggiungere algebricamente agli istanti di un fenomeno
osservato dal suolo terrestre quando si voglia evitare un residuo errore periodico prodotto dalla variazione della
distanza fra la Terra e l'oggetto osservato, a causa del moto di rivoluzione del nostro pianeta intorno al Sole.
Essendo un effetto indotto dal moto della Terra lungo l'eclittica e dalla velocità non infinita della luce, tale correzione
può assumere valori da 0, per oggetti posti ai poli dell'eclittica, a +/- 8m 19s per un astro giacente, apparentemente,
sull'eclittica stessa (vedi figura sotto).
Solitamente espressa in decimali di giorno, tale correzione può essere calcolata a partire da formule diverse a seconda
della precislone richiesta. Fino a pochi anni fa erano normalmente utilizzate apposite tabelle come quelle di Landolt e
Blondeau, comparse originariamente in una pubblicazione dell'Osservatorio della Louisiana ma riprese in seguito in altre
pubblicazioni; oggigiorno, però, si preferisce fornire semplici programmi per piccoli e grandi computer: chi fosse
interessato può riceverne una versione adatta al proprio rivolgendosi alla Sezione Software della UAI.
Una versione semplificata, la cui precisione dipende dall'accuratezza a cui ci si voglia spingere nel fissare certi
parametri, in grado comunque di garantire scarti non superiori a +/- 20s (più che sufficienti per osservazioni fotografiche
o visuali) è data dalla seguente formula, proposta da Binnendijk nel 1960:
Corr. Elioc. = -0d,0057755 x [R cos (cos
(cos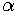 cos
cos ) + R sin
) + R sin (sin
(sin  sin
sin + cos
+ cos cos
cos sin
sin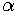 )]
)]
dove: R è la distanza Terra-Sole (espressa in UA, unità astronomiche) alla data considerata;
 è la longitudine celeste del Sole per tale giorno;
è la longitudine celeste del Sole per tale giorno;
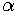 è l'ascensione retta della stella espressa in gradi (si ricorda che, 1h di AR è pari a 15°);
è l'ascensione retta della stella espressa in gradi (si ricorda che, 1h di AR è pari a 15°);
 è la declinazione della stella;
è la declinazione della stella;
 è l'obliquità dell'eclittica.
è l'obliquità dell'eclittica.
In prima approssimazione è possibile porre R=1,  =23°,441; per
=23°,441; per 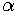 e
e
 si prendano le coordinate equatoriali della stella quali risultano da un catalogo di posizione,
o dallo stesso catalogo generale delle stelle variabili, senza procedere alla correzione per la precessione degli equinozi.
Per quanto riguarda
si prendano le coordinate equatoriali della stella quali risultano da un catalogo di posizione,
o dallo stesso catalogo generale delle stelle variabili, senza procedere alla correzione per la precessione degli equinozi.
Per quanto riguarda  il cui calcolo non è immediato, ci si può rifare ad un almanacco della UAI
che anzi riporta giornalmente i valori di R,
il cui calcolo non è immediato, ci si può rifare ad un almanacco della UAI
che anzi riporta giornalmente i valori di R,  , nonché di R cos
, nonché di R cos e
R sin
e
R sin , chiamati rispettivamente X ed Y o coordinate rettangolari del Sole.
, chiamati rispettivamente X ed Y o coordinate rettangolari del Sole.
Ma quando occorre la correzione eliocentrica? Praticamente ogni qualvolta sia un necessario conoscere l'istante di un
evento con una precisione migliore di  8m. Tipici casi sono le RR Lyrae o altre variabili con periodi
pari od inferiori al giorno.
8m. Tipici casi sono le RR Lyrae o altre variabili con periodi
pari od inferiori al giorno.
A questo proposito sarà forse utile precisare che tutte le effemeridi di stelle variabili indicano sempre il tempo
eliocentrico degli eventi (l'istante cioè che risulterebbe ad un osservatore posto al centro dei Sole) per cui quando si
voglia effettuare uno studio sulle variazioni degli istanti osservati e calcolati dalle effemeridi per una variabile rapida
(es. istanti dei massimi e dei minimi) è d'obbligo applicare la correzione eliocentrica alle proprie osservazioni. Anzi,
a puro titolo di curiosità, ricorderemo come questa correzione possa rivelarsi del tutto insufficiente nel caso di eventi
estremamente rapidi (come le pulsar) o di variabili per le quali possa avere comunque significato una precisione migliore di
 5s. Come si è visto, infatti, nella correzione eliocentrica si fa riferimento alla distanza fra il
centro della Terra e quello del Sole supponendo il nostro pianeta in rotazione intorno a quest'ultimo; in realtà, non è
esatto dire che la Terra ruota attorno al centro del Sole, ma è più esatto affermare che Terra, pianeti e lo stesso Sole,
ruotano attorno al centro di massa del Sistema Solare, per cui è stata proposta dall'IAU (International Astronomical Union)
l'adozione del Tempo Baricentrico.
5s. Come si è visto, infatti, nella correzione eliocentrica si fa riferimento alla distanza fra il
centro della Terra e quello del Sole supponendo il nostro pianeta in rotazione intorno a quest'ultimo; in realtà, non è
esatto dire che la Terra ruota attorno al centro del Sole, ma è più esatto affermare che Terra, pianeti e lo stesso Sole,
ruotano attorno al centro di massa del Sistema Solare, per cui è stata proposta dall'IAU (International Astronomical Union)
l'adozione del Tempo Baricentrico.
La posizione del baricentro del nostro sistema planetario varia periodicamente al variare delle posizioni reciproche dei
pianeti e del Sole: il termine principale è dato dal periodo siderale di Giove (pari a circa 12 anni) che fa oscillare la
correzione baricentrica di  4,5 s. A tali livelli di precisione si rivelano non più trascurabili nemmeno
le oscillazioni mensili della posizione della Terra, indotte dalla rotazione della stessa attorno al centro di massa del
sistema Terra-Luna (
4,5 s. A tali livelli di precisione si rivelano non più trascurabili nemmeno
le oscillazioni mensili della posizione della Terra, indotte dalla rotazione della stessa attorno al centro di massa del
sistema Terra-Luna ( 0,015s) e della rotazione diurna della Terra attorno al proprio asse (valore
massimo
0,015s) e della rotazione diurna della Terra attorno al proprio asse (valore
massimo  0,021s nei pressi dell'equatore).
0,021s nei pressi dell'equatore).

Significato della correzione eliocentrica: per l'osservatore posto in A lo stesso evento che ha luogo sulla stella S,
appare prodursi quasi 17 minuti dopo rispetto al tempo misurato da un ipotetico osservatore che si trovi in B.
Il ritardo è dovuto alla differente distanza degli osservatori dalla stella. Con la correzione eliocentrica si riferiscono
i tempi ad un osservatore posto al centro del Sole.
Definizione tratta dall'articolo "Astroagenda" di Pietro Baruffetti, pubblicata a pagina 54 de l'Astronomia n° 76
(aprile 1988); ringrazio l'autore e l'editore per la gentile concessione.
 (cos
(cos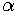 cos
cos ) + R sin
) + R sin (sin
(sin  sin
sin + cos
+ cos cos
cos sin
sin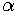 )]
)] è la longitudine celeste del Sole per tale giorno;
è la longitudine celeste del Sole per tale giorno; 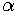 è l'ascensione retta della stella espressa in gradi (si ricorda che, 1h di AR è pari a 15°);
è l'ascensione retta della stella espressa in gradi (si ricorda che, 1h di AR è pari a 15°); è la declinazione della stella;
è la declinazione della stella; è l'obliquità dell'eclittica.
è l'obliquità dell'eclittica.
 8m. Tipici casi sono le RR Lyrae o altre variabili con periodi
pari od inferiori al giorno.
8m. Tipici casi sono le RR Lyrae o altre variabili con periodi
pari od inferiori al giorno.
